Issue 2 - INTRODUCTION TO CANCER BIOLOGY: THE SOMATIC MUTATION THEORY

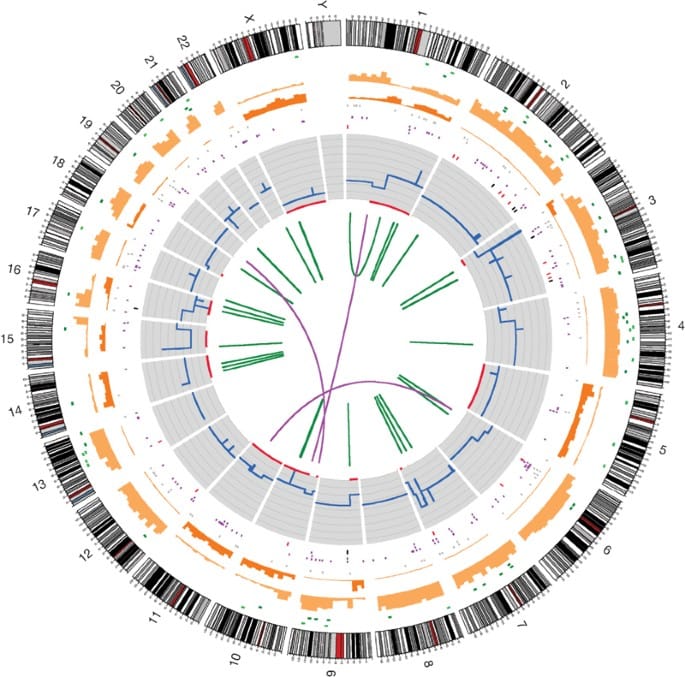
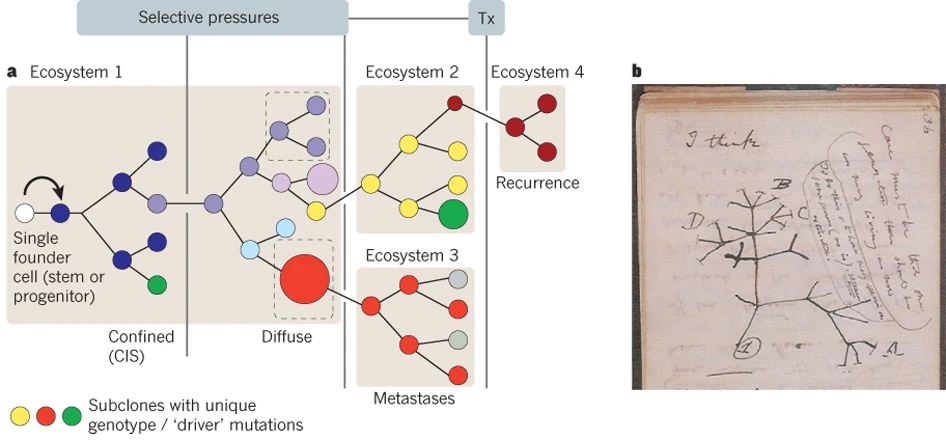
.... Cancer is a Darwinian, somatic evolutionary process driven by the sequential accumulation of genetic and structural alterations in individual cells. This is the cancer gene theory AKA somatic mutation theory that was first theorised by Peter Nowell in 1976. It posits that a subset of the gained alterations provides a heritable selective advantage, enhancing proliferation, survival, or adaptability thereby increasing the frequency of these clones within the tissue ecosystem. Over time, through cycles of mutation and selection, a dynamic tumour population emerges, comprising subclones whose composition changes in response to internal pressures and external therapies (see following figure).

Introduction

The DNA duplex was once considered a stable macromolecule. Not anymore. We now know that during replication, human DNA exhibits an estimated error rate of approximately 1 × 10⁻⁹ per base pair per cell division, equating to roughly one mutation per genome duplication. Yes, this reflects an error rate but it also demonstrates remarkable fidelity given the scale of the genome. Such precision in replication arises from the several overlapping DNA repair systems, including base-excision repair, mismatch repair, nucleotide-excision repair, and double-strand break repair, that collectively maintain genomic stability and suppress mutagenesis. When these systems fail or are overwhelmed, mutations accumulate, altering the balance of cellular growth and differentiation and laying the foundation for oncogenesis.

Mutations

Mutations form the mechanistic basis of cancer. While most are biologically neutral, a small subset i.e. driver mutations, confer selective advantages that fuel proliferation, survival, and adaptation. By contrast, passenger mutations represent neutral variants that accumulate through drift, forming the noisy genomic background of tumours (Stratton, Campbell & Futreal, 2009). Discerning these drivers from passengers remains one of the major analytical challenges in cancer genomics and sequencing-based analysis.

Intratumoral heterogeneity compounds this challenge, as distinct subclones with unique genotypes and phenotypes evolve along divergent trajectories, driving variable therapeutic responses (Gerlinger et al., 2012). The tumour microenvironment adds another layer of complexity: stromal and immune cells obscure tumour-specific signals, while local selective pressures—nutrient gradients, hypoxia, and immune surveillance—continually reshape clonal evolution (Hanahan, 2022). Thus, cancer progression reflects not just intrinsic genomic alterations but their dynamic interaction with the surrounding ecosystem, rendering sequencing-based interpretation profoundly complex.

As a result, although data generation in modern cancer genomics is increasingly becoming routine; interpretation, remains one of the most complex challenges in biomedicine. I will explain this further in future newsletters.

History of somatic mutation theory

The somatic mutation theory is obvious to us today. But it came on the back of some amazing findings. The story goes as follows.

In 1960, Peter Nowell and David Hungerford identified a small abnormal chromosome consistently present in chronic myeloid leukaemia (CML)—the Philadelphia chromosome. Janet Rowley (1973) later demonstrated that this abnormality resulted from a reciprocal translocation between chromosomes 9 and 22 [t(9;22)(q34;q11)], producing the BCR–ABL fusion gene, which encodes a constitutively active tyrosine kinase. This was the first definitive link between a chromosomal rearrangement and human cancer, transforming Theodor Boveri’s early cytogenetic theories into a mechanistic and evolutionary model of tumour progression (Nowell & Hungerford, 1960; Rowley, 1973).

These findings established that mutation drives selection, and selection fuels clonal expansion—a unifying principle of tumour evolution. Modern sequencing efforts have extended this framework by revealing mutational signatures, quantitative fingerprints of DNA damage and repair processes such as UV-induced pyrimidine dimers, tobacco carcinogens, APOBEC cytidine deamination, and CpG deamination (Alexandrov et al., 2013). SMT thus integrates molecular, cytogenetic, and evolutionary observations into a cohesive theory of cancer development and provides the conceptual foundation for precision oncology, which aims to predict and therapeutically exploit the evolutionary logic of tumours.

The Axioms of Somatic Mutation Theory: A Quantitative Foundation

The somatic mutation theory (SMT) of cancer rests upon several fundamental axioms that can be expressed in quantitative, population-genetic terms. These principles allow us to translate biological intuition about mutation and selection into the mathematical language that underpins evolutionary dynamics. For anyone seeking to understand cancer as an evolutionary disease, these axioms are indispensable.

Axiom 1: Mutations occur stochastically at a context-dependent per-base, per-division rate, μ(x).

In cancer, the most common and biologically relevant form of genetic alteration is the single nucleotide variant (SNV), or point mutation. Although related to single nucleotide polymorphisms (SNPs), the distinction is crucial: SNVs arise as random, somatic events without implications for inheritance, while SNPs represent germline variants maintained in populations through evolutionary time.

An equally important distinction must be drawn between mutation rate and mutation frequency. The mutation rate (μ) refers to the likelihood that a mutation occurs during DNA replication i.e., the probability per base per division. The mutation frequency, by contrast, refers to the proportion of mutant alleles within a population of cells — a quantity that depends on selection, drift, and cellular proliferation history.

Thus, this first axiom can be restated as follows: the rate of mutational errors is not fixed but depends on sequence context, replication mode, chromatin state, and environmental mutagens. Factors such as CpG methylation, replication timing, and exposure to reactive oxygen species or ultraviolet light all influence μ(x) (Alexandrov et al., 2013; Helleday et al., 2014).

If we denote μ_b(x) as the somatic mutation rate per base per cell division at genomic position x (of order ~10⁻⁹ in most human somatic tissues) and L_g as the length of the gene’s mutable region (e.g., coding exons or regulatory hotspots), then the per-gene mutation rate per division is given by:

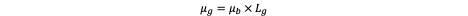
This equation states that the per-gene mutation probability is simply the product of the number of mutable bases and the probability that any given base mutates

Now, if a tissue compartment contains N susceptible cells, each undergoing t rounds of division, the total number of cell-division events is N·t. The expected number of independent mutations occurring within a specific gene across that tissue is therefore:

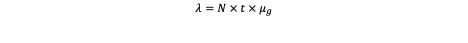
Up to this point, we have merely scaled the per-gene mutation rate to the tissue level - no conceptual leap, simply an application of probability across a population of dividing cells. Assuming that mutation events occur independently and are rare, they can be modeled as a Poisson process. The probability that at least one such mutation arises within the tissue is therefore:

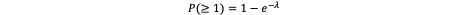
This expression formalizes the intuitive notion that the likelihood of a mutational “hit” increases with both tissue size and cell turnover. It also explains why rapidly dividing tissues — such as colonic crypts or hematopoietic stem cell compartments — exhibit substantially higher mutation burdens than more quiescent tissues like neurons or cardiac muscle.

This first axiom, thus, provides a quantitative bridge between molecular processes (DNA replication and repair) and evolutionary outcomes (the emergence of variation upon which selection acts). The next axioms, will extend this reasoning to incorporate the stochastic survival of mutant lineages, selection coefficients, and the branching-process approximations that describe clonal expansion — linking molecular mutation rates to observable patterns of tumour evolution.

Axiom 2: Fitness Effects Are Heritable at the Cellular Level

For a somatic mutation to influence tumour evolution, it must not only occur (as described in Axiom 1) but also persist. Most mutations are lost quickly due to stochastic drift, cell death, or competition among neighbouring cells. Only a small subset of mutations evade this early extinction and give rise to enduring lineages — an event quantified by the fixation probability (π_est). In population-genetic terms, fixation probability represents the likelihood that the frequency of a particular allele within a population ultimately reaches unity (100%). In the somatic context, this corresponds to the local dominance of a mutant clone within its tissue microenvironment.

To formalize this, consider the selective advantage (s) of a newly arisen mutation. If each wild-type cell produces, on average, W offspring per generation, then a mutant cell with a fitness advantage produces W(1 + s) offspring, where s > 0 denotes a beneficial mutation.

Thus, the relative fitness of the mutant to the wild-type is (1 + s). Fitness effects in this framework are heritable at the cellular level, meaning that any phenotypic trait conferred by a mutation (e.g., increased proliferation, reduced apoptosis, or altered metabolism) is transmitted to all descendant cells.

Within this quantitative framework, J. B. S. Haldane (1927) derived a seminal result that remains foundational for modern somatic evolution models. Working within a branching-process approximation, he demonstrated that for mutations with a small selective advantage (s ≪ 1) in a large, well-mixed population, the probability that a single copy of a beneficial mutation survives early stochastic loss is approximately 2s. In other words, while the majority of newly arisen beneficial mutations are lost to random drift (with probability roughly 1 − 2s), a fraction ≈ 2s successfully establish persistent lineages. This relationship provides a powerful yet intuitive insight that even modestly advantageous mutations can dominate given sufficient cell divisions and time.

Haldane’s approximation was later generalized by Motoo Kimura (1957, 1962) using diffusion models of allele frequency dynamics and this unified stochastic and deterministic perspectives of evolution. Under the Haldane–Kimura framework, the fixation (or establishment) probability of a single advantageous mutation can be expressed as:

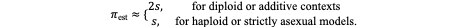
In the context of somatic evolution, where cells divide asexually and selection acts on cellular phenotypes rather than organisms, this relationship underpins the Stochastic Genetic Theory (SGT) of tumour progression. Mutations occur randomly (Axiom 1), but their persistence and expansion depend on the balance between stochastic loss and selection on fitness-altering traits. Beneficial mutations that alter the cell’s proliferative capacity, resistance to apoptosis, or metabolic efficiency are more likely to evade extinction and establish expanding clones.

Together, these dynamics define the bridge between molecular mutation processes and clonal evolution. The heritability of fitness effects allows mutations to act as units of selection within the somatic landscape, leading to the emergence of subclonal heterogeneity and intratumoural diversity. This framework, initially articulated by Nowell (1976) and later formalized by Beerenwinkel et al. (Nature Reviews Genetics, 2016), provides the mathematical and conceptual foundation for modern cancer evolutionary theory — linking the random generation of somatic mutations to the deterministic patterns of clonal expansion observed in sequencing data from The Cancer Genome Atlas (TCGA) and related large-scale genomic efforts.

Axiom 3: Population Dynamics Approximate Branching Processes

Tumour cell populations do not grow deterministically; rather, they follow stochastic birth–death dynamics governed by probabilistic rules of replication, death, and mutation. This stochasticity means that at any given point, some mutant lineages will go extinct while others expand, a behaviour that can be accurately modelled using branching processes (Kendall, 1948; Nowell, 1976). Within this framework, cell birth and death are treated as probabilistic events influenced by a selection coefficient (s), which quantifies the relative fitness advantage (or disadvantage) conferred by a mutation. Axiom 3 therefore provides the critical quantitative link between population genetics and tumour biology: it demonstrates how the somatic mutation process (Axiom 1) and heritable fitness effects (Axiom 2) jointly determine the clonal composition of a tissue.

To illustrate this with realistic order-of-magnitude reasoning, let us consider conservative estimates derived from human somatic tissues. The per-base per-division mutation rate (μb) is approximately 1 × 10⁻⁹ — a consensus value across many somatic lineages (remember I told you to remember this number) (Lynch, 2010; Tomasetti & Vogelstein, Science, 2015). For a typical coding gene of L_g ≈ 1500 bp, the per-gene mutation rate per cell division becomes:

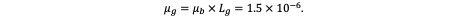
Now suppose a large epithelial compartment contains N = 10⁸ susceptible cells, each undergoing t = 1 division. The expected number of independent mutational events (λ) hitting that gene during this single round of division is:

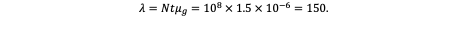
Hence, across the entire compartment, ~150 independent mutations in that gene are expected per division cycle. The probability that at least one such event occurs — assuming a Poisson distribution of rare events — is:

In other words, given the scale of cell populations, it is almost certain that at least one mutational event will occur at that locus per division cycle.

Next, consider a typical driver mutation with a modest selective advantage of s = 0.01 (1% fitness benefit). Using the Haldane small-s approximation (π_est≈ 2s), the establishment probability per mutation is approximately 0.02. The expected number of established driver clones from that gene during this division window is therefore:

Thus, even with conservative assumptions, several independent clones can become established per gene per round of division. The implications are striking: extremely low per-base mutation rates, when multiplied by tissue scale, yield a constant stream of potentially selectable variants. Small fitness advantages, acting through the laws of branching processes, suffice to generate measurable clonal heterogeneity - a key proof-of-principle for the Somatic Genetic Theory (SGT).

With this simple but powerful quantitative reasoning we have explained why multicellular tissues, composed of billions of dividing cells, naturally accumulate multiple independent driver lineages over time. Each lineage’s fate depends on stochastic drift, local selection, and microenvironmental constraints, leading to the mosaic clonal architectures observed in human tumours.

References

Alexandrov, L. B., et al. (2013). Signatures of mutational processes in human cancer. Nature, 500, 415–421.
Beerenwinkel, N., et al. (2016). Cancer evolution: Mathematical models and computational inference. Nature Reviews Genetics, 17, 703–718.
Gerlinger, M., et al. (2012). Intratumor heterogeneity and branched evolution revealed by multiregion sequencing. New England Journal of Medicine, 366, 883–892.
Greaves, M. & Maley, C. (2012). Clonal evolution in cancer. Nature, 481, 306–313. doi:10.1038/nature10762
Haldane, J. B. S. (1927). A mathematical theory of natural and artificial selection. Proceedings of the Cambridge Philosophical Society, 23, 607–615.
Hanahan, D. (2022). Hallmarks of cancer: New dimensions. Cell, 185, 15–40.
Helleday, T., et al. (2014). Mechanisms underlying mutational signatures in human cancers. Nature Reviews Genetics, 15, 585–598.
Hoeijmakers, J. H. J. (2009). DNA damage, aging, and cancer. New England Journal of Medicine, 361, 1475–1485.
Kimura, M. (1957). Some problems of stochastic processes in genetics. Annals of Mathematical Statistics, 28, 882–901.
Kimura, M. (1962). On the probability of fixation of mutant genes in a population. Genetics, 47, 713–719.
Lindahl, T. (1993). Instability and decay of the primary structure of DNA. Nature, 362, 709–715.
Lynch, M. (2010). Rate, molecular spectrum, and consequences of human mutation. Proceedings of the National Academy of Sciences, 107, 961–968.
Nowell, P. C. (1976). The clonal evolution of tumour cell populations. Science, 194, 23–28.
Nowell, P. C. & Hungerford, D. A. (1960). A minute chromosome in human chronic granulocytic leukemia. Science, 132, 1497.
Rowley, J. D. (1973). A new consistent chromosomal abnormality in chronic myelogenous leukemia identified by quinacrine fluorescence and Giemsa staining. Nature, 243, 290–293.
Stratton, M. R., Campbell, P. J. & Futreal, P. A. (2009). The cancer genome. Nature, 458, 719–724.
Tomasetti, C. & Vogelstein, B. (2015). Variation in cancer risk among tissues can be explained by the number of stem cell divisions. Science, 347, 78–81.